---
format:
  moan-livro-html:
    css: css/jogovel.css
       
include-after-body:
  text: |
    <script src="jogovel.js"></script>
    <script src="https://js.livro.online/moan-quarto/leitor-web.min.js"></script>
    <script src="js/ajuste-legenda-figura.js"></script>
    <link rel="stylesheet" type="text/css" href="https://js.livro.online/moan-quarto/css/configuracoesleitor.min.css" />
---

# Atividades lúdicas <br />para o ensino da <br />linguagem algébrica

::: autores
Eliza Bruna Dalla Corte Andreolla^[1](#footnote-14){#footnote-ref-14}^ <br />
Fernanda Guerra^[2](#footnote-15){#footnote-ref-15}^ <br />
Thais de Souza^[3](#footnote-16){#footnote-ref-16}^ <br />
Adriana Schawabe Reis Lepreda^[4](#footnote-17){#footnote-ref-17}^
:::

## Objetivo geral

Propor atividades que auxiliem, principalmente professores do sétimo ano
do Ensino Fundamental, no ensino e na aprendizagem da linguagem
algébrica.

## Introdução

O ensino da linguagem algébrica tem sido um grande desafio a ser
trabalhado no sétimo ano do Ensino Fundamental. E, como afirma Pereira
[-@pereira_2017], esse assunto é muitas vezes apresentado aos estudantes de forma
descontextualizada e por meio de exercícios de fixação mecânicos, o que
causa barreiras e dificulta ainda mais o ensino e a aprendizagem desse
conteúdo, contribuindo para a aversão à matemática. Com objetivo de
auxiliar a apresentação desse tema de forma clara e dinâmica aos alunos
do sétimo ano, este trabalho apresenta atividades que introduzem o uso
da linguagem algébrica, de forma lúdica, buscando atingir o interesse
dos alunos pelo assunto, favorecendo então, a aprendizagem de fato.

## Atividade 1: <br />uso de cartões coloridos

### Objetivo

Introduzir a linguagem algébrica e as operações de adição e subtração de
polinômios de forma pictórica.

### Material

-   Papel cartão ou cartolina de duas cores diferentes;
-   Tesoura;
-   Caneta.

### Preparação

No papel cartão, desenhe e recorte em duas cores, grupos de figuras com,
pelo menos, três formatos diferentes. O objetivo é que cada figura
simbolize uma incógnita e as cores representem valores positivos e
negativos.

### Procedimento

#### Primeira parte

Exponha para os alunos certa quantidade de figuras de mesma cor, mas com
formatos diferentes. Peça para que escrevam a quantidade de cada formato
de figura observada. Repita o procedimento quantas vezes achar
necessário. As Figuras [-@fig-31] e [-@fig-32] exemplificam duas situações possíveis. A
resposta esperada para a situação representada pela Figura [-@fig-31] é 4
estrelas e 4 corações. Para a situação representada pela Figura [-@fig-32] a
resposta esperada é 3 losangos e 7 corações. 

:::: {.grid}

::: {.g-col-6}
![Corações e Estrelas](img/fig31.jpg){#fig-31 fig-alt="Corações e estrelas de cartolima ma cor
verde." loading="lazy" style="width:230px; height: auto;"}
:::

::: {.g-col-6}
![Corações e Losangos](img/fig32.jpg){#fig-32 fig-alt="Corações e losangos de cartolina na cor
verde." loading="lazy" style="width:230px; height: auto;"}
:::

::::

Estimule os alunos a trocar os nomes das figuras (corações, losangos e
estrelas) por uma notação mais "rápida" e simples, utilizando, por
exemplo, a inicial da palavra de cada figura. Assim, as respostas para
as situações representadas pelas Figuras [-@fig-31] e [-@fig-32] seriam, 4E e 4C, e 3L e
7C, respectivamente.

Após a substituição dos nomes das figuras por letras, é natural trocar o
conectivo "e" pelo sinal de adição, já que em outras palavras, está
havendo uma soma. Nas Figuras [-@fig-31] e [-@fig-32], temos, nessa ordem, 4 estrelas e 5
corações e 3 losangos e 7 corações, que seriam denotados como 4E + 4C e
3L + 7C, respectivamente. Nesse instante, é conveniente dizer aos
estudantes que não é possível somar figuras diferentes, podendo usar
como justificativa o fato de possuírem formatos diferentes. Portanto,
usando esse mesmo raciocínio na nova notação, ressalta-se que não devem
ser somadas ou subtraídas letras (incógnitas) diferentes.

#### Segunda parte

Nesse momento, a proposta é trabalhar com formatos de figuras em duas
cores diferentes^[5](#footnote-18){#footnote-ref-18}^, uma cor
representando valores positivos e outra cor representando valores
negativos. Por exemplo, trabalhar com figuras na cor verde e na cor
vermelha^[6](#footnote-19){#footnote-ref-19}^. As figuras de cor verde
representarão valores positivos e carregarão o sinal +, as de cor
vermelha representarão valores negativos e carregarão o sinal -.

Nessa etapa da atividade, o objetivo é levar o aluno a compreender a
adição algébrica. Antes de trabalhar com a linguagem matemática, porém,
sugere-se mostrar aos alunos que, por exemplo, cada figura vermelha
"anula" uma figura verde, desde que sejam de mesmo formato.
Primeiramente, apresente grupos de figuras e deixe que os alunos
"descubram o resultado" sozinhos. Deixe-os livres para registrar, ou
não, a quantidade de figuras. Repita o processo até perceber que os
alunos o compreenderam.

Posteriormente, comece a utilizar a notação matemática. Apresente
novamente aos alunos um ou mais grupos de figuras. Peça para anotarem as
quantidades de cada figura, respeitando os valores positivos e
negativos.

:::: {.grid}

::: {.g-col-6}
![C. L. vermelho e verde](img/fig33.jpg){#fig-33 fig-alt="Corações e losangos de cartolina, sendo alguns na cor verde e outros
na cor vermelha." loading="lazy"}
:::

::: {.g-col-6}
![C. L. vermelho e verde](img/fig34.jpg){#fig-34 fig-alt="Corações e losangos de cartolina, sendo alguns na cor verde e outros
na cor vermelha." loading="lazy"}
:::

::::

Nas Figuras [-@fig-33] e [-@fig-34] são apresentados exemplos dessa situação. Na [@fig-33]
há 5 corações verdes, 4 corações vermelhos, 1 losango verde e 3 losangos
vermelhos. Usando pensamento análogo à primeira parte da atividade,
denota-se a quantidade de figuras da seguinte maneira: (+5C) + (-4C) +
(+1L) + (-3L). É natural que, nesse momento, os alunos encontrem um
pouco de dificuldades com a representação matemática, por isso, é
importante repetir o processo da notação e deixar claro o porquê do uso
dos parênteses, para que isso não se torne um obstáculo futuramente.

Após a representação da situação em linguagem algébrica, manuseando as
figuras e relembrando a atividade anterior, na qual figuras iguais e de
cores diferentes se anulam, deve ser mostrado aos alunos que duas
figuras de mesmo formato, mesmo que de cores diferentes, podem e devem
ser somadas. Dessa forma, realizando a soma, obtém-se em linguagem
algébrica um total de 1C para os corações, já que + 5C + (- 4C) = 1C, e
para os losangos -2L, pois + 1L + (- 3L) = - 2L. Os losangos e corações
ainda pertencem ao mesmo grupo, então devemos somá-los, tem-se 1C + (-
2L) = 1C -- 2L.

Repetindo o mesmo processo com a [@fig-34] (4 corações positivos e 5
corações negativos, 1 losango positivo e 3 losangos negativos), tem-se +
4C + (- 5C) + 1L + (- 3L) = -1C -2L.

#### Terceira parte

A partir deste ponto, pode-se começar a estipular um "valor" para cada
formato de figura, colocando uma certa quantidade de pontos em cada uma
delas, como na @fig-35.

![Losangos com valores](img/fig35.jpg){#fig-35 fig-alt="Losangos verdes de cartolina com quatro pontos
dentro" loading="lazy"}

Agora, não será mais contado apenas a quantidade de figuras existentes,
e sim a quantidade de pontos que há nesse conjunto de figuras. Iniciando
pela quantidade de losangos que aparece na @fig-35, tem-se 9 losangos
ou 9L. Observe que 1 losango possui 4 pontos. Como são 9 losangos e em
cada um há 4 pontos, é possível calcular a quantidade total de pontos do
conjunto dessa figura, multiplicando a quantidade total de losangos pela
quantidade de pontos que cada losango possui, logo 9 x 4 = 36, ou seja,
juntando todos os losangos será obtido um total de 36 pontos.

![Losangos e Estrelas com valores](img/fig36.jpg){#fig-36 fig-alt="Losangos e estrelas verdes de cartolina com pontos dentro. Os losangos têm um ponto e as estrelas, dois" loading="lazy"}

Pode-se realizar o mesmo exercício com mais de um formato de figura. Na @fig-36, tem-se 4 estrelas e 4 losangos, ou seja, 4E + 4L. Observando a quantidade de pontos de cada figura (1 losango vale 2 pontos, 1 estrela,
1 ponto, algebricamente: L = 2 e E = 1), pode-se calcular o valor total
do conjunto:

4E = 4 x 1 = 4 e 4L = 4 x 2 = 8

4E + 4L = 4 + 8 = 12

Portanto, 12 será a quantidade total de pontos na [@fig-36].

A mesma atividade pode ser realizada utilizando valores negativos como,
por exemplo, na [@fig-37]{.nobreak}:

![Corações e losangos com valores positivos e negativos](img/fig37.jpg){#fig-37 fig-alt="Corações e losangos de cartolina com pontos dentro. Cada coração
possui quatro pontos dentros, já os losangos, 3 pontos cada. Existem
losangos verdes e também vermelhos, assim como, os corações também podem
ser verde ou vermelhos." loading="lazy"}

O processo de resolução é análogo ao anterior, envolvendo todas as
discussões apresentadas no decorrer das três etapas da atividade.

## Atividade 2: <br />jogo do alvo

A atividade foi inspirada na proposta de Sirlei Miguel [-@miguel_2014] em seu
caderno desenvolvido no Programa de Desenvolvimento Educacional (PDE),
um programa promovido pela Secretaria de Estado da Educação do estado do
Paraná.

### Objetivo

Trabalhar as operações de adição e subtração com os números inteiros.

### Material

-   Cartolina branca;
-   Compasso;
-   Tinta ou lápis de cor;
-   Lápis de escrever ou caneta;
-   Feijão.

### Preparação

Para confeccionar o alvo, que será no formato circular, pegue uma
cartolina branca e desenhe 5 circunferências concêntricas, sendo a maior
com raio de 15 cm. Cada faixa formada pela delimitação das
circunferências, ficará com 3 cm de largura. Pinte cada uma delas com
cores distintas, a sua escolha^[7](#footnote-20){#footnote-ref-20}^.
Usaremos, como exemplo, as cores: vermelho, rosa, amarelo, azul-claro e
azul-escuro^[8](#footnote-21){#footnote-ref-21}^, como ilustrado na
[@fig-38]{.nobreak}. Depois de pintado, recorte o alvo sobre a circunferência
maior.

![Coloração do alvo](img/fig38.jpg){#fig-38 fig-alt="Círculo colorido com as cores variando da fronteira até o centro:
vermelho, rosa, amarelo, azul claro e azul escuro. Não é um
degradê." loading="lazy"}

Para construir a borda lateral do alvo (que ficará como uma caixa
circular), desenhe em uma cartolina branca um retângulo de 94 cm de
comprimento e 4 cm de largura. Em uma das arestas menores, acrescente um
retângulo de 4 cm por 2 cm (usado para colar uma aresta a outra) e, em
uma das arestas maiores, acrescente um retângulo de 94 cm por 1 cm
(usado para colar a borda no alvo), como no molde da [@fig-39]{.nobreak}. Cole a
faixa lateral no alvo.

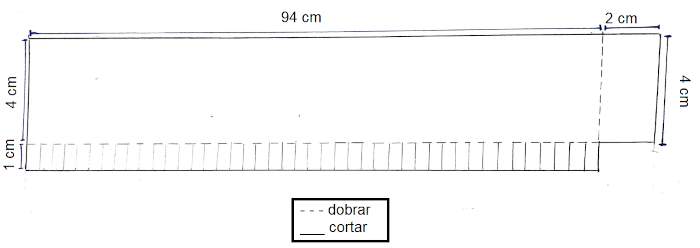![Molde da faixa lateral do alvo](img/fig39.png){#fig-39 fig-alt="Molde com marcações de medidas e indicações de onde cortar e dobrar." loading="lazy"}

Uma sugestão, para facilitar o processo da construção do alvo, é
utilizar a tampa de uma embalagem de pizza. Ao final, ele deverá ficar
como no exemplo, ilustrado na @fig-310.

![Alvos](img/fig310.jpg){#fig-310 fig-alt="Círculo colorido com as cores variando da fronteira até o centro:
vermelho, rosa, amarelo, azul claro e azul escuro. Não é um
degradê" loading="lazy"}

### Como jogar

Os jogadores ou a pessoa que estiver aplicando o jogo, deverão estipular
um valor correspondente a cada faixa colorida, por exemplo, 5 pontos
para cada feijão que cair sobre a faixa azul-escuro, 1 ponto para a
azul-claro, 4 pontos na faixa amarela, 3 para a rosa e 2 pontos para a
faixa vermelha. Cada jogador, na sua vez, joga no alvo 15 feijões. Em
seguida, deve contar quantos feijões caíram em cada uma das faixas do
alvo e registrar em uma tabela a quantidade de feijões e os pontos
correspondentes. Os jogadores podem jogar quantas rodadas quiserem ou
determinarem entre si, de modo que todos joguem a mesma quantidade,
sempre fazendo as respectivas anotações.

Para facilitar as anotações, é conveniente induzir os alunos para que
escolham uma única letra ou símbolo para representar cada faixa. É
importante que as anotações estejam organizadas de modo a auxiliar os
cálculos ao final da brincadeira. Pode ser construído um quadro para tal
finalidade.

Por exemplo, se na primeira rodada um aluno acertar 2 feijões na faixa
azul-escuro, 3 na faixa azul-claro, 5 na faixa amarela, 1 na faixa rosa
e 4 na faixa vermelha, e usar E para azul-escuro, C para azul-claro, A
para amarelo, R para rosa e V para vermelho, pode anotar da seguinte
forma:

| Rodada  |  Soma dos feijões |
|:-------:|:------------------:|
|  Primeira | 2E + 3C + 5A + 1R + 4V|
|  Segunda  |   | 
|  Terceira |   |  
|  Quarta   |   |  
|  Quinta   |   |  
|  Sexta    |   |  
|  Sétima   |   |

: Expressões de cada rodada {#tbl-expressoes}

Ao final das rodadas, cada jogador calcula seu total de pontos. Vence
quem tiver maior pontuação.

:::{.callout-tip}
Quando for conveniente, atribua valores negativos para algumas faixas,
para introduzir a adição e a subtração com números inteiros.
:::

## Atividade 3: <br />jogo de memória

Esse jogo foi baseado na proposta de Beatriz Rechia da Silva [-@silva_2012] em
seu caderno desenvolvido no Programa de Desenvolvimento Educacional
(PDE), um programa promovido pela Secretaria de Estado da Educação do
estado do Paraná.

### Objetivo

Explorar e relacionar a linguagem algébrica com a linguagem corrente por
meio de um jogo.

### Material

Dois grupos distintos de cartelas, variando a forma de apresentar as
expressões algébricas. Em um grupo, as expressões devem ser escritas por
extenso e, no outro, deve-se usar a linguagem algébrica:

| Escrito por Extenso  |  Linguagem Algébrica |
|:--------------------:|:--------------------:|
| O dobro de um número |  $2x$ |
| A diferença entre dois números |    $a - b$ |
| Metade de um número  |  $x/2$ |
| A diferença entre um número e 2  |  $z - 2$ |
|  A soma de dois números diferentes |  $g + y$ |
| A quinta parte de um número |  $x/5$ |
| Um número mais 1 |  $x + 1$ |
| Um número mais ele mesmo | $x + x = 2x$ |
| O triplo de um número | $3x$ |
| Um número menos ele mesmo | $x - x = 0$ |
| Um número somado com o dobro de outro número | $c + 2d$ |
| Um número multiplicado por ele mesmo três vezes | $x \cdot x \cdot x= x^3$ |
| A soma de três números consecutivos | $x + (x + 1) + (x + 2)$ |                                                       

: Linguagem corrente e linguagem algébrica {#tbl-algebrica}

Devido a pandemia da COVID-19, pensou-se em atividades que pudessem ser
desenvolvidas de maneira remota, assim, foi desenvolvido uma versão
*online* desse jogo. Ele encontra-se disponível em:

[]{#jogo_memoria}

### Acesso à atividade

::: {.content-visible when-format="html"}
[Acessar](https://puzzel.org/pt/memory/play?p=-MekRbcdmNkkpY9jp_7c){.btn_book target="blank"}
:::

::: {.content-visible when-format="pdf"}
<https://puzzel.org/pt/memory/play?p=-MekRbcdmNkkpY9jp_7c>
:::

Caso não esteja disponível, acesse a adaptação feita pela editora com base nas informações e nas questões apresentadas nesta proposta didática:

::: {.content-visible when-format="html"}

```{=html}

<button class="jogo_da_memoria_pdf_jm" onclick="abrir_jogo_da_memoria_pdf_jm()">Abrir Jogo da Memória</button>

<audio id="sucesso_pdf_jm" src="https://upload.wikimedia.org/wikipedia/commons/2/23/Sucesso.ogg"></audio>
<audio id="erro_pdf_jm" src="https://upload.wikimedia.org/wikipedia/commons/6/6d/Som_de_Erro.ogg"></audio>
<audio id="fim_de_jogo_pdf_jm" src="https://upload.wikimedia.org/wikipedia/commons/c/c1/Deslizando_o_dedo_no_piano.ogg"></audio>
<audio id="virando_a_carta_pdf_jm" src="https://upload.wikimedia.org/wikipedia/commons/4/4f/Virada_de_Carta.ogg"></audio>





<div id="container_pdf_jm">


<div id="info_pdf_jm">

    <button class="iniciar_pdf_jm" onclick="voltar_tela_inicial_pdf_jm()">&#x21bb;</button>

    <button class="som_pdf_jm" onclick="toggle_som_pdf_jm()">&#9835;</button>
    
    <div id="jogador1_pdf_jm"><span class="nome_pdf_jm">Jogado da Memória</span><span class="pontuacao_pdf_jm"></span></div><div id="jogador2_pdf_jm"><span class="nome_pdf_jm"></span><span class="pontuacao_pdf_jm"></span></div>

    <button class="fechar_pdf_jm" onclick="abrir_jogo_da_memoria_pdf_jm()">&#10005;</button>

</div>

<div class="tela_inicial_pdf_jm">

    <h3>Jogo da Memória</h3>

    <div>

        <label style="cursor:pointer;">
            <input type="radio" name="numJogadores_pdf_jm" value="1" checked>
            1 Jogador
        </label>
        
        <label style="cursor:pointer;">
            <input type="radio" name="numJogadores_pdf_jm" value="2">
            2 Jogadores
        </label>
	
	</div>

    <div id="entrar_nomes_pdf_jm">

        <label>
            <input type="text" id="nomeJogador1_pdf_jm" placeholder="Nome do Jogador 1 (opcional)">
        </label>
        
        <div id="nomeJogador2_pdf_jmContainer_pdf_jm" style="display:none">
            <label>
                <input type="text" id="nomeJogador2_pdf_jm" placeholder="Nome do Jogador 2 (opcional)">
            </label>
        </div>
	
    </div>
	<div>

        <button class="fechar_pdf_jm" onclick="abrir_jogo_da_memoria_pdf_jm()">Fechar</button>

        <button id="botaoJogar" class="iniciar_pdf_jm" onclick="iniciar_pdf_jm()">Jogar</button>

    </div>

</div>

<div id="container_cartas_pdf_jm">

    <div class="tela_final_pdf_jm"><div></div><button  onclick="fechar_tela_final_pdf_jm()">Ok</button></div>
    
    <div id="0" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="1" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="2" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="3" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="4" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="5" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="6" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="7" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="8" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="9" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="10" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="11" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="12" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="13" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="14" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="15" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="16" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="17" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="18" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="19" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="20" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="21" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="22" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="23" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="24" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    <div id="25" class="carta_pdf_jm" ><div class="carta_interior_pdf_jm " onclick="virarCarta(this)"><button class="fechar_pdf_jm">✕</button><div class="frente_pdf_jm"></div><div class="verso_pdf_jm"><span>Para efetuar a compra de uma tv no valor de R$ 1420,00, José recebeu um desconto de R$ 426,00 no pagamento à vista. Qual a fração que representa a porcentagem de desconto?</span></div></div></div>
    

</div>

    
</div>

```

:::

### Como jogar

Divida a sala em grupos de 2 a 3 alunos; cada jogador, na sua vez,
desvira dois cartões, um azul^[9](#footnote-22){#footnote-ref-22}^ e um
branco. Se o cartão azul traduzir o que está escrito no cartão branco o
jogador fica com os dois cartões. Se o cartão azul não traduzir o que
está escrito no cartão branco, ambos devem ser virados, permanecendo nos
mesmos lugares em que estavam antes, de forma similar a um jogo de
memória.

Ao terminar os cartões, cada jogador conta seus pontos de acordo com os
números de cartões que acumulou.

## Considerações finais

A matemática possui particularidades na sua linguagem, sendo até mesmo
considerada como uma disciplina alfabetizadora. A linguagem algébrica
exige um acentuado grau de abstração por parte dos alunos que,
comumente, apresentam dificuldades. É um conteúdo a ser trabalhado com
os alunos de sétimo ano do Ensino Fundamental e que tem se apresentado
como um grande desafio, pois muitas vezes é desenvolvido de forma
descontextualizada e mecânica, criando nos alunos uma aversão pela
matemática [@pereira_2017].

Desenvolver o pensamento algébrico é algo que pode ser iniciado desde a
Educação Infantil, para que, à medida que o aluno avance na
escolarização, seu pensamento seja potencializado para desenvolver uma
linguagem algébrica mais apropriada [@pereira_2017].

Neste trabalho, apresentamos três sugestões de atividades que podem ser
desenvolvidas em sala de aula. Os materiais podem ser confeccionados
pelos próprios alunos. Por meio destes jogos é possível introduzir a
linguagem algébrica, apresentar as operações de adição e subtração de
polinômios, adição e subtração com os números inteiros e relacionar a
linguagem algébrica com a linguagem corrente.

É importante ressaltar que os jogos não devem ser utilizados como única
forma de trabalhar a linguagem algébrica, mas são ótimos auxiliares para
a apresentação ou mesmo a fixação dos conteúdos. Além disso, eles
contribuem para aumentar o interesse dos alunos pelo conteúdo,
favorecendo a aprendizagem.

## Notas

1.  ::: {#footnote-14}
    Acadêmica do curso de Matemática Unioeste/Cascavel. Bolsista do
    Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
    E-mail:elizadcorte@outlook.com [↑](#footnote-ref-14)
    :::

2.  ::: {#footnote-15}
    Acadêmica do curso de Matemática Unioeste/Cascavel. Bolsista do
    Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
    E-mail: nandaguerra_22@hotmail.com [↑](#footnote-ref-15)
    :::

3.  ::: {#footnote-16}
    Acadêmica do curso de Matemática Unioeste/Cascavel. Bolsista do
    Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
    E-mail: thaissouza38@hotmail.com [↑](#footnote-ref-16)
    :::

4.  ::: {#footnote-17}
    Professora Supervisora do subprojeto Interdisciplinar
    Matemática/Química, do Programa Institucional de Bolsas de Iniciação
    à Docência (Pibid), da Unioeste. E-mail: adrilepreda@gmail.com
    [↑](#footnote-ref-17)
    :::

5.  ::: {#footnote-18}
    Procure usar um aplicativo ou um site de simulação de cores para
    daltônicos. A ideia é evitar que alguém não consiga distinguir uma
    cor da outra. [↑](#footnote-ref-18)
    :::

6.  ::: {#footnote-19}
    Essas cores, nas tonalidades usadas, funcionam para daltônicos. Se o
    leitor quiser alterá-las, lembre-se de usar *websites* ou *app* que
    simulem os diferentes tipos de daltonismo, de forma a não usar cores
    que não são distinguidas por daltônicos. [↑](#footnote-ref-19)
    :::

7.  ::: {#footnote-20}
    Procure usar um aplicativo ou um site de simulação de cores para
    daltônicos. A ideia é evitar que alguém não consiga distinguir uma
    cor da outra. [↑](#footnote-ref-20)
    :::

8.  ::: {#footnote-21}
    Essas cores, nas tonalidades usadas, funcionam para daltônicos. Se o
    leitor quiser alterá-las, lembre-se de usar *websites* ou *app* que
    simulem os diferentes tipos de daltonismo, de forma a não usar cores
    que não são distinguidas por daltônicos. [↑](#footnote-ref-21)
    :::

9.  ::: {#footnote-22}
    Nesse nosso exemplo é azul, no entanto, a cor pode ser qualquer uma.
    Mas lembre-se de usar simuladores para daltonismo, a fim de que a
    escolha das cores não inviabilize o jogo para os daltônicos.
    [↑](#footnote-ref-22)
    :::

## Referências