# O uso do astrolábio caseiro no
ensino da trigonometria
$$\newcommand{\sen}{\mathrm{sen}\thinspace}\newcommand{\tg}{\mathrm{tg}\thinspace}$$
::: autores
Bruna Eduarda Unser^[1](#footnote-23){#footnote-ref-23}^
Eduardo Rossoni Zeni^[2](#footnote-24){#footnote-ref-24}^
Fabiana Magda Garcia Papani^[3](#footnote-25){#footnote-ref-25}^
:::
## Objetivo geral
Esta proposta didática propõe a construção de um astrolábio caseiro e a
utilização desse instrumento para realização de um experimento de
medições, simulando o trabalho, por exemplo, de geógrafos, agrimensores
ou astrônomos. Os resultados obtidos nessas medições serão utilizados
para ensinar trigonometria. A proposta também prevê a inserção do uso de
planilhas eletrônicas como ferramenta para o ensino de trigonometria.
## Introdução
A trigonometria (TRI + GONO + METRIA que significa TRÊS + ÂNGULOS +
MEDIDA), é "\[\...\] parte da matemática que tem como objeto de estudo
os lados e os ângulos de um triângulo" [@leite_2016, p. 15]. Surgiu com
as necessidades práticas oriundas da astronomia, agrimensura, navegação,
entre outras ciências. Para solucionar problemas, como por exemplo,
calcular as alturas das pirâmides ou a largura dos rios, os
cientistas^[4](#footnote-26){#footnote-ref-26}^ dessas áreas se baseavam
em dois conceitos matemáticos básicos: a razão entre dois números e
semelhança de triângulos.
Segundo Boyer [@boyer_2001], a trigonometria não foi obra de um só homem, nem
de um só povo, e seus primeiros indícios apareceram no Egito e na
Babilônia. No Egito, rudimentos de trigonometria aparecem a partir da
revolução agrícola, quando o homem começou a demarcar terras, fixar
propriedade e formas de plantio, gerando a necessidade de saber qual o
tamanho do terreno, por exemplo. Na Babilônia, além da agricultura, a
evolução da trigonometria se deu pelo trabalho dos astrônomos, que
durante muitos anos mediram os movimentos dos astros.
O astrolábio, cuja origem do nome provém do grego *astrolabion*, foi um
instrumento desenvolvido e aprimorado durante séculos por diversos povos
com base em teorias aritméticas, trigonométricas, astrológicas e
geográficas. Quando do seu surgimento, tinha como função resolver
problemas relacionados à navegação, ao deslocamento e temporalidade dos
astros, a medir a altura de objetos de difícil acesso, entre outras
aplicações.
Autores discutem sobre o surgimento exato ou até mesmo a inexistência de
uma história completamente linear e definida de tal instrumento. No
entanto, sua presença em diversas culturas e regiões distantes umas das
outras demonstra seu movimento, utilização, bem como seu papel
científico e social. No contexto islâmico, por exemplo, o indivíduo que
sabia utilizar o astrolábio era considerado uma pessoa importante e
possuir um astrolábio era sinal de poder político e religioso [@saraiva_2016].
::: bloco-imagem
{#fig-41 fig-alt="Astrolábio Esférico" loading="lazy"}
[Fonte:]{.figure-caption} @brian
:::
Com o passar dos anos, os instrumentos criados pelos antepassados foram
sofrendo melhorias em seus mecanismos, se adequando às necessidades e
isso não foi diferente com o astrolábio. O instrumento passou por
diversas versões até chegar no que temos hoje. Podemos ver, na [[@fig-41]]{.nobreak}, o
astrolábio esférico. Este possuía discos, nos quais pontuavam-se as
latitudes, longitudes, horizonte, mapa astrológico e movimento do sol.
Esses adornos possibilitavam a descoberta de características do tempo e
do espaço, tais como dias, estações e partilhas geográficas durante todo
o ano. Devido às mudanças de contextos históricos e de realidade e,
ainda, pelo fato deste instrumento ser muito pesado e complexo,
dificultando seu uso, este astrolábio caiu em desuso, sendo substituído
por uma versão mais leve e simplificada, baseada na projeção
estereográfica. O astrolábio planisférico, o qual podemos observar na
[@fig-42], é capaz de resolver problemas sem precisar recorrer à
trigonometria esférica. Nos séculos XV e XVI, o astrolábio plano foi
simplificado dando origem ao astrolábio náutico, o qual foi amplamente
utilizado no continente europeu [@fantuzzi]. Veja [@fig-43]. A
invenção do relógio de pêndulos e de instrumentos científicos como o
telescópio fez do astrolábio um instrumento obsoleto e atualmente
astrolábios são construídos apenas por curiosidade, diversão ou para
fins educacionais [@morrison].
::: bloco-imagem
{#fig-42 fig-alt="Astrolábio Planisférico" loading="lazy"}
[Fonte:]{.figure-caption} [@sailko]
:::
::: bloco-imagem
{#fig-43 fig-alt="Astrolábio Náutico" loading="lazy"}
Fonte: [@skoklosters]
:::
Essa proposta didática abordará a construção de uma versão caseira do
astrolábio e a realização de experimentos com a sua utilização para
ensinar trigonometria. Vários autores relatam que atividades práticas em
sala de aula, utilizando o astrolábio, têm trazido bons resultados para
uma aprendizagem com significado da trigonometria. Campos [-@campos_2017], por
exemplo, apresenta um relato de experiência, no qual constrói o
astrolábio e o utiliza em atividades práticas com o objetivo de estudar
conceitos de razões trigonométricas com alunos do 1º ano do Ensino
Médio. O autor conclui que a abordagem teórica tradicional aliada às
atividades práticas contribui para que o aluno perceba a matemática na
sua vida e não apenas nos livros ou na escola. Soriano, Silva e
Damasceno [@soriano] colocam que a ressignificação de conteúdos obsoletos,
por meio da utilização da história da matemática em sala de aula,
instiga a curiosidade dos alunos e mostra o processo de criação dos
conceitos matemáticos. Saito [-@saito_2016] salienta que quando o professor
reintegra o conteúdo matemático ao processo histórico, ele consegue
propor novas estratégias de ensino, dando outro significado à
matemática, mostrando que a matemática é uma construção humana, que
ocorreu aos poucos, com erros, aproximações e, então, pequenos acertos,
desconstruindo a visão de uma ciência construída por formas
adivinhatórias completas e por poucos homens sábios.
Além disso, ao utilizar o astrolábio para realizar medições,
trabalharemos com a experimentação em sala de aula. Segundo Lorenzato [2010 *apud* @almeida_2019], "experimentar é valorizar também a construção do conhecimento em vez do resultado dele, pois mais
importante que conhecer a solução é saber como encontrá-la. Tal aspecto
desperta o interesse do discente e favorece a aprendizagem com
significado".
As atividades de experimentação sugeridas nessa proposta didática estão
propositalmente organizadas de forma a aumentar o grau de dificuldade do
conteúdo abordado e permitir o avanço dos conteúdos da trigonometria,
até que em um determinado momento, é introduzida a utilização de
planilhas eletrônicas como ferramenta facilitadora do ensino desse
conteúdo. De acordo com Silva e Moraes [-@silva_2016], as planilhas eletrônicas
se relacionam bem com a matemática e estão repletas de ferramentas que
proporcionam uma aula bastante dinâmica e atrativa, deixando os alunos
mais interessados pela disciplina e, consequentemente, alcançando o
resultado esperado. Saldanha [-@saldanha_2016] ressalta que as atividades
utilizando planilhas eletrônicas, além de tornar as aulas mais
atrativas, permitem que os alunos se concentrem no raciocínio e na
programação, ao invés de efetuar cálculos muitas vezes entediantes.
## Atividade 1:
construção do astrolábio caseiro
Pretendemos --- com a construção do astrolábio --- desenvolver a
criatividade, a interatividade entre os alunos e o professor e promover
o interesse pela história por trás do objeto construído e pelo estudo da
trigonometria.
### Materiais e métodos
A construção do astrolábio requer os seguintes materiais: um canudo ou
tubo de caneta; um pedaço de arame; fio de *nylon* ou barbante; um
transferidor; fita adesiva e um objeto que sirva de peso, como metal ou
uma pedra. Observem a [@fig-44].
::: bloco-imagem
{#fig-44 fig-alt="Materiais para a construção: canudo, tubo de caneta, pedaço de arame,
barbante, transferidor, fita adesiva e um pedaço de
metal." loading="lazy"}
:::
Para construir o astrolábio, deve-se --- com um alicate ou algum objeto
similar --- segurar o arame, aquecê-lo e fazer um furo no centro do
transferidor, ou seja, sobre a reta com a marcação de 90°, como
apresentado na [@fig-45]. Em seguida, é necessário cortar e amarrar um
pedaço de barbante no furo realizado e amarrar na outra extremidade do
barbante o objeto escolhido como peso. Por fim, deve-se fixar o canudo
sobre o transferidor, paralelo à reta que contém as marcações 0° e 180º,
observe a [@fig-46].
::: bloco-imagem
{#fig-45 fig-alt="Furando o transferidor" loading="lazy"}
:::
::: bloco-imagem
{#fig-46 fig-alt="Canudo fixado nas marcações 0º e 180º" loading="lazy"}
:::
## Atividade 2:
medições com o astrolábio
### Método de uso
O objetivo é utilizar o astrolábio construído para realizar medições de
alturas inacessíveis, simulando o trabalho de um topógrafo, por exemplo,
e utilizar a dinâmica para a facilitar a compreensão dos conceitos de
trigonometria, tais como: seno, cosseno e tangente de ângulos notáveis;
relações trigonométricas em um triângulo retângulo; adição e subtração
de arcos; apresentar aplicações desses conceitos matemáticos em outras
ciências e no nosso cotidiano, mostrando que a matemática, assim como
outras ciências, é desenvolvida pouco a pouco.
O primeiro passo para utilizar o astrolábio é definir o objeto de
estudo. Tendo realizado a escolha, deve-se enxergar pelo canudo o topo
do objeto escolhido como ilustrado na [@fig-47].
::: bloco-imagem
{#fig-47 fig-alt="Modo de usar o astrolábio caseiro. Uma pessoa ao ar livre, em um gramado, usando o astrolábio caseiro para medir um prédio" loading="lazy"}
:::
Em seguida, deve-se observar o ângulo demarcado pelo astrolábio, o qual
chamaremos de α (*alfa*). Para isso, basta verificar a marcação
determinada pelo barbante sobre o transferidor.
::: bloco-imagem
{#fig-48 fig-alt="Uma imagem contendo pessoa, edifício, ao ar livre, usando o astrolábio caseiro para medir." loading="lazy"}
:::
Se chamarmos de θ (*teta*) o ângulo complementar ao ângulo *α*, ou seja,
o ângulo que somado a *α* resulta em 90° ([@fig-48]), podemos observar na
[[@fig-49]]{.nobreak} que o cateto oposto a *θ* é $h$ (a altura do objeto menos a
altura do observador) e que o cateto adjacente a este mesmo ângulo é a
distância $(d)$ entre o observador e o objeto. Assim, devemos também
medir a altura do observador e a distância entre o mesmo e o objeto
escolhido para estudo.
::: bloco-imagem
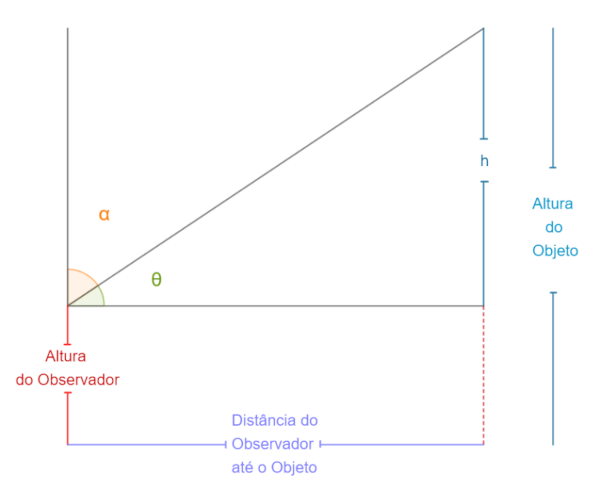{#fig-49 fig-alt="Esquema gráfico da medição, mostrando alfa, teta, a altura do
observador, a altura do objeto e a distância do observador até o objeto." loading="lazy"}
:::
Desta forma, a altura do objeto é obtida por meio da aplicação da
relação ([-@eq-tg]) abaixo, relação métrica no triângulo retângulo baseada na
tangente do ângulo *θ* e, portanto, relaciona os catetos oposto e
adjacente a este ângulo.
$$\tg\theta = \frac{h}{d}$${#eq-tg}
Considere $h$ a altura do objeto menos a altura do observador e $d$
é a distância entre o observador e o objeto.
Uma vez que conhecemos o ângulo θ, a altura do observador e a distância
entre o observador e o objeto, temos na relação dois elementos
conhecidos e apenas a altura do objeto desconhecida.
### Medindo uma árvore
Para calcular a altura da árvore, seguimos os passos definidos
anteriormente. Primeiramente, tomou-se a distância da árvore ao observador e com a
utilização do astrolábio demarcou-se o ângulo *α* --- formado entre o
canudo e o barbante --- e calculou-se o ângulo complementar $\theta$.
Em seguida, com uma trena, mediu-se a distância entre a árvore e o
observador e a altura do observador.
::: bloco-imagem
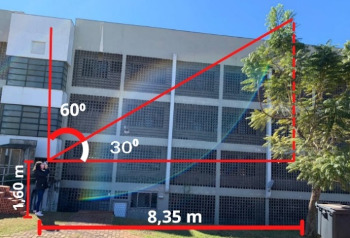{#fig-410 fig-alt="Imagem ao ar livre com um gramado, um prédio, uma árvore e uma pessoa
usando o astrolábio caseiro para medir a altura da árvore. Sobre a
imagem há marcações em vermelho mostrando as medidas obtidas: os ângulos
alfa e teta, a altura do observador e a distância do observador até a
árvore. A altura da árvore desde a cabeça do observador até o topo é uma
linha pontilhada." loading="lazy"}
:::
Nesse exemplo, como exibido na [@fig-410], os resultados obtidos foram,
$\alpha = 60^\circ$ e consequentemente $\theta = 30^\circ$, a
distância entre o observador e a árvore foi de $8,35 \thinspace m$ e
a altura do observador $1,60 \thinspace m$.
Ao término das medições, os alunos voltam à sala de aula e o professor
utiliza os resultados das observações para introduzir ou aplicar
conceitos de trigonometria.
Podemos observar que nesta primeira situação o ângulo $\theta$ é o
ângulo notável, de $30^\circ$, cuja tangente mede
$\frac{\sqrt{3}}{3}$. Os ângulos $30^\circ$, $45^\circ$ e
$60^\circ$ são chamados ângulos notáveis por suas aparições em
vários problemas matemáticos e, assim, é importante conhecer os valores
do seno, cosseno e tangente desses ângulos. Desta forma, utilizando a
relação (1), temos que,
$$\tg30^\circ =\frac{h}{8,35}$$
Utilizando $0,5773$ como valor aproximado para tangente de $30^\circ$ e realizando as
devidas manipulações, temos que,
$$h = 0,5773 \cdot 8,35 = 4,82 \thinspace m$$
Para sabermos a altura da árvore, basta somarmos o valor encontrado com
a altura do observador, deste modo,
Altura da árvore = $4,82 + 1,60 = 6,42 \thinspace m$
### Medindo uma porta
O objetivo deste experimento é:
::: bloco-imagem
{#fig-411 fig-alt="Uma menina usando o astrolábio caseiro para medir uma porta. É uma
área aberta, mas coberta e com sombra." loading="lazy"}
:::
- Medir um objeto acessível, para poder comparar o resultado da medida
utilizando o astrolábio com a medida obtida em uma medição
convencional. Escolhemos para isso uma porta, como mostra a [[@fig-411]]{.nobreak}.
- Provocar uma situação didática na qual o ângulo $\theta$ não é um ângulo
notável, de modo a dar continuidade, em sala de aula, ao ensino da
trigonometria, apresentando algumas relações trigonométricas.
Realizamos o procedimento de medição como anteriormente, no caso da
árvore. Obtivemos para este objeto as medidas: $2,60 \thinspace m$ de distância do observador à porta, o ângulo demarcado no astrolábio foi $75^\circ$ e, portanto, seu ângulo complementar é $15^\circ$. Neste caso o ângulo encontrado não é um ângulo notável, mas pode ser obtido como a diferença entre dois ângulos
notáveis. Sendo assim, podemos calcular sua tangente utilizando a
relação entre a tangente da diferença e a tangente dos arcos, a
saber:
$$\tg(a-b) = \frac{\tg a -\tg b}{1+\tg a \cdot \tg b}$${#eq-tgdif}
Podemos expressar o ângulo de $15^\circ$ como $45^\circ - 30^\circ$. Assim, uma vez que a tangente de $30^\circ$ é
$\frac{\sqrt{3}}{3}$ e a tangente de $45^\circ$ é $1$, temos,
utilizando a equação ([-@eq-tgdif]),
$$
\begin{aligned}
\tg(15^\circ) &= \tg(45^\circ - 30^\circ) \\[10pt]
&= \frac{1 -\frac{\sqrt{3}}{3}}{1 + 1 \cdot \frac{\sqrt{3}}{3}} \\[10pt]
&= \frac{\frac{3 - \sqrt{3}}{3}}{\frac{3 + \sqrt{3}}{3}} \\[10pt]
&= \frac{3 - \sqrt{3}}{3 + \sqrt{3}}
\end{aligned}
$$
Neste momento, podemos efetuar uma racionalização e encontrar
$$\begin{aligned} \tg(15^\circ) &= \frac{3 - \sqrt{3}}{3 + \sqrt{3}}\cdot \frac{3 + \sqrt{3}}{3 + \sqrt{3}} \\[10pt]
&= \frac{12 - 6\sqrt{3}}{6} = 2 - \sqrt{3} \\[10pt]
& \approx 0,2679 \end{aligned}$$
Assim $h = 0,2679 \cdot2,60 = 0,6965 \thinspace m$.
Para sabermos a altura da porta, basta somarmos o valor encontrado com a
altura do observador $(1,60 \thinspace m)$, deste modo a altura da
porta é $2,2965 \thinspace m$.
Cabe ressaltar que a altura da porta obtida pela medição convencional,
isto é, medindo a porta como uma trena é de $2,30 \thinspace m$.
Logo, podemos notar que a medida obtida utilizando o astrolábio fornece
um resultado muito próximo a altura real da porta, sendo que a diferença
obtida se deve às aproximações realizadas e a possíveis imprecisões nas
medições.
Podemos aproveitar o contexto gerado pelo experimento para explorar o
seno, cosseno ou tangente de arcos e as relações entre seno, cosseno e
tangente da soma, ou diferença, dos respectivos arcos, tais como as
apresentadas na Tabela 1.
Tabela 1 -- Relações entre seno, cosseno e tangente da soma e/ou
diferença de arcos e os respectivos arcos
| |
|:---:|
| $\sen(a + b) = \sen a \cdot \cos b + \sen b \cdot \cos a$ |
| $\sen(a - b) = \sen a \cdot \cos b - \sen b \cdot \cos a$ |
| $\cos(a + b) = \cos a \cdot \cos b - \sen a \cdot \sen b$ |
| $\cos(a - b) = \cos a \cdot \cos b + \sen a \cdot \sen b$ |
| $\tg(a + b) = \frac{\tg a + \tg b}{1 - \tg a \cdot \tg b}$ |
| $\tg(a - b) = \frac{\tg a - \tg b}{1 + \tg a \cdot \tg b}$ |
Podemos, ainda, explorar os conceitos de racionalização, bem como de
valor aproximado (arredondamento), números racionais e irracionais.
### Medindo um prédio
::: bloco-imagem
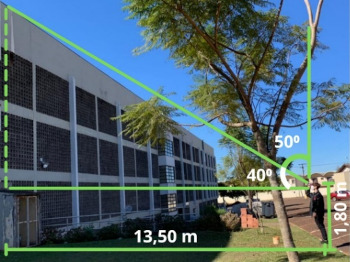{#fig-412 fig-alt="Imagem ao ar livre com um gramado, um prédio, uma árvore e uma pessoa
usando o astrolábio caseiro para medir a altura do prédio. Sobre a
imagem há marcações em verde mostrando as medidas obtidas: os ângulos
alfa e teta, a altura do observador e a distância do observador até a
árvore. A altura do prédio desde a cabeça do observador até o topo é uma
linha pontilhada." loading="lazy"}
:::
O objetivo desse experimento foi criar uma situação diferente das
geradas nos dois casos anteriores. Neste caso o ângulo θ não é um ângulo
notável, tão pouco pode ser obtido por meio da soma ou subtração de
ângulos notáveis. Sendo assim, abordaremos a possibilidade de utilizar
planilhas eletrônicas. Escolhemos, para realizar o experimento, medir a
altura de um prédio. Como nos casos anteriores, foram medidos o ângulo α
com ajuda do astrolábio, a distância entre o observador e o prédio e a
altura do observador, como podemos ver na [@fig-412].
O ângulo marcado no transferidor foi $\alpha = 50 ^\circ$, porém,
devemos lembrar que este ângulo é o complementar do ângulo formado pela
linha de visão do observador e o solo. Assim, o ângulo entre a linha de
visão do observador e o solo é $\theta = 40 ^\circ$. Temos também
que a distância entre o observador e o objeto é $ d = 13,50 \thinspace
m $ e que a altura do observador é $ h = 1,80 \thinspace m $.
Quando voltarmos para a sala de aula e utilizar os resultados das
medições, observaremos que neste experimento, o ângulo encontrado não é
um ângulo notável e não conseguimos obtê-lo a partir da soma ou
diferença de ângulos notáveis. Portanto, exploraremos o uso de
calculadora ou planilhas eletrônicas como, por exemplo, o Excel (2020),
para o cálculo de valores das funções trigonométricas. O Excel
disponibiliza as funções *sen, cos* e *tan*, que fornecem,
respectivamente o seno, o cosseno e a tangente de um ângulo dado em
radianos. Neste momento cabe abordar a questão das diferentes unidades
de medida que podem ser utilizadas para medir ângulos e a relação entre
elas. Nas calculadoras científicas, por exemplo, devemos escolher qual
unidade de medida (radianos, grau ou grado) vamos utilizar. No Excel,
por exemplo, se digitarmos "$\sen(30)$"", o aplicativo irá retornar o
valor -0,98803. O leitor distraído pode achar que o software realizou um
cálculo errado, pois sabe que seno de $30^\circ$ é $0,5$. O
acontece é que o Excel entende o argumento "$30$"" como $30$
radianos, que equivale aproximadamente $1719^\circ$, que é um arco
situado no quarto quadrante.
Assim, se optamos por utilizar o Excel e desejamos retornar o valor do
seno (cosseno, tangente) de um ângulo dado em graus, devemos primeiro
transformá-lo em radianos, utilizando a função *radianos*. Por exemplo,
para calcular o seno de $30^\circ$, podemos digitar no Excel $\sen(\text{radianos}(30))$ e então o Excel retornará o valor $0,5$.
Retornando ao nosso problema, podemos utilizar a função para encontrar
$\tg 40^\circ = 0,8391$.
Assim, utilizando a relação ([-@eq-tg]), obtemos
$$h = 0,8391 \cdot 13,50 = 11,33 \thinspace m$$.
Para sabermos o valor da altura do prédio, basta somarmos $h$ com a altura do observador, obtendo que a altura do prédio é $13,12 \thinspace m$.
Destacamos que por ocasião deste experimento, o professor, em sala de
aula, além de explorar a utilização de planilhas eletrônicas como
ferramenta para o ensino, neste caso da trigonometria, pode explorar a
relação entre as unidades de medida de ângulo, grau e radianos, o sinal
das funções seno, cosseno e tangente em cada um dos quadrantes e o
(de)crescimento dessas funções trigonométricas, de modo que, o aluno,
conhecendo os valores dessas funções para os ângulos notáveis, possa
avaliar a coerência da resposta retornada pelo software.
## Considerações finais
Acredita-se que as atividades apresentadas nesta proposta didática
permitirão a utilização de aspectos da história da matemática para
ensinar conceitos de trigonometria, corroborando com a opinião de
diversos autores de que ao utilizar a história da matemática como
ferramenta didática, estamos proporcionando mais do que um recurso
informativo. Essa metodologia permite mostrar aos alunos uma matemática
em construção, portanto fruto da invenção humana. Permitirá ainda uma
abordagem diferente para o conteúdo de trigonometria, com as atividades
práticas, possibilitando a percepção de que a trigonometria pode ser
utilizada em atividades cotidianas. Por último, a proposta didática
estimula e exemplifica a utilização de planilhas eletrônicas em sala de
aula. Essa prática, além de colocar os alunos em contato com uma
ferramenta muito presente na vida cotidiana, permite que os alunos
desenvolvam os cálculos mais rapidamente, podendo dar maior atenção às
ideias e conceitos presentes na atividade.
## Notas
1. ::: {#footnote-23}
Acadêmica do Curso de Matemática -- Unioeste/Cascavel-PR. Bolsista
do Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
E-mail: bruna.unser@unioeste.br [↑](#footnote-ref-23)
:::
2. ::: {#footnote-24}
Acadêmico do Curso de Matemática -- Unioeste/Cascavel-PR. Bolsista
do Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
E-mail: Eduardo.zeni1@unioeste.br [↑](#footnote-ref-24)
:::
3. ::: {#footnote-25}
Professora do Curso de Matemática -- Unioeste/Cascavel. Colaboradora
de área do subprojeto Interdisciplinar Matemática/Química, do
Programa Institucional de Bolsas de Iniciação à Docência (Pibid), da
Unioeste. E-mail: [↑](#footnote-ref-25)
:::
4. ::: {#footnote-26}
"Cientistas" e "Ciências" estão sendo usadas em um sentido amplo
neste texto. Questionamentos como "Existia ciência na antiguidade?"
não fazem parte do escopo deste trabalho. [↑](#footnote-ref-26)
:::
## Referências