# Números inteiros {.unnumbered}
::: autores
Erika Diana Alves de Oliveira^[1](#footnote-4){#footnote-ref-4}^
Ricardo Mondini Ferrazza^[2](#footnote-5){#footnote-ref-5}^
Thamara Tobaldini^[3](#footnote-6){#footnote-ref-6}^
Dulcyene Maria Ribeiro^[4](#footnote-7){#footnote-ref-7}^
:::
## Objetivo
O objetivo desta proposta didática é promover a compreensão das
operações de adição e subtração de números inteiros. As atividades
sugeridas utilizam fichas coloridas para representarem quantidades
positivas e negativas e jogos que envolvem as operações com números
inteiros. Acreditamos que uma vez compreendidas as regras envolvidas nos
jogos, ficará mais fácil entender as regras das operações com números
inteiros, pois os raciocínios são análogos.
## Introdução
Quando cursamos a disciplina de Didática Aplicada ao Ensino da
Matemática, do curso de Licenciatura em Matemática da Universidade
Estadual do Oeste do Paraná (Unioeste), elaboramos uma sequência
didática que tinha como objetivo contribuir com a superação dos
obstáculos didáticos e epistemológicos presentes no ensino dos números
inteiros. Na sequência didática elaborada, optamos por trabalhar com
materiais manipulativos, por compreendermos que o uso de materiais
didáticos auxilia em um processo de ensino e aprendizagem com
significado.
Segundo Lorenzato (2006, p.18), "Material didático (MD) é qualquer
instrumento útil ao processo de ensino-aprendizagem. Portanto, MD pode
ser um giz, uma calculadora, um filme, um livro, um quebra-cabeça, um
jogo \[\...\]". Dentre os MD para o trabalho com números inteiros,
destacamos o ábaco dos números inteiros que, segundo os Parâmetros
Curriculares Nacionais, é um recurso interessante para explorar tal
assunto.
> \[\...\] para explorar a adição e subtração, outro recurso
> interessante é o ábaco de inteiros, que consiste em duas varetas
> verticais fixadas num bloco, nas quais se indica a que vai receber as
> quantidades positivas e a que vai receber as quantidades negativas,
> utilizando argolas de cores diferentes para marcar pontos. Esse
> material permite a visualização de quantidades positivas e negativas e
> das situações associadas ao zero: varetas com a mesma quantidade de
> argolas. Ao manipular as argolas nas varetas, os alunos poderão
> construir regras para o cálculo com os números inteiros [@pcn_1998, p. 99].
No desenvolvimento da atividade, nos deparamos com uma limitação do
material ao realizar a operação de subtração, pois os alunos, naquele
momento, não possuíam conhecimento da regra dos sinais para representar
a operação no ábaco. O ábaco utilizado possuía duas hastes, uma para as
quantidades positivas e outra para as negativas. Na adição, as
quantidades negativas eram representadas todas na haste negativa e as
quantidades positivas eram representadas todas na haste positiva. Em
seguida, anulava-se as argolas positivas com as negativas e o resultado
era representado na haste que, após a anulação, ainda tivesse argolas.
Na subtração, o aluno necessariamente deveria realizar a troca de sinais
antes de representar as quantidades nas hastes, no exemplo
$(-7)-(-2)$, se o aluno seguisse a mesma ideia da adição, os dois
números deveriam ir à haste negativa, mas na operação de subtração
devemos representar sete argolas na haste negativa e duas argolas na
haste positiva, ficando com $(-7)+(2)$. Assim, não conseguimos
realizar a operação no ábaco sem aplicar a regra dos sinais antes da
representação.
Com esses questionamentos e reflexões em mente, analisamos livros e
artigos desenvolvidos na área que trabalham com o ensino de números
inteiros, a fim de elaborar uma proposta que corresponda com o ensino
que esperamos oferecer. Assim, desenvolvemos a presente proposta
didática.
## Os obstáculos no ensino de números inteiros
Estudos como o de Igliori [-@igliori_nocao_1999] e Pommer [-@pommer_1998] apontam que o aluno
passa por diversas dificuldades no processo de construção do conceito de
números negativos, decorrentes de obstáculos epistemológicos.
De acordo com Schubring [-@schubring_desenvolvimento_2009, p. 18], os obstáculos epistemológicos
"residem na natureza do conhecimento matemático, razão pela qual não
podem ser evitados, já que são constitutivos dos respectivos
conhecimentos e identificados na história dos conceitos".
Para Igliori,
> A noção de obstáculo pode ser utilizada tanto para analisar a gênese
> histórica de um conhecimento como o ensino ou a evolução espontânea do
> aluno. Pode-se, portanto pesquisar os obstáculos epistemológicos a
> partir de uma análise histórica ou a partir de dificuldades
> resistentes entre os alunos procurando confrontá-las [@igliori_nocao_1999, p. 98].
Existem diversos obstáculos epistemológicos no ensino, entre eles
Igliori [-@igliori_nocao_1999] aponta a noção de números inteiros. Para a autora, a
aceitação dos números negativos demorou para se consolidar, pois
enfrentou diversos obstáculos. Segundo Radford [1997 *apud* @igliori_nocao_1999], isso se deu devido às culturas locais e pela concepção de
ciências, matemática e objetos dessas culturas. Enquanto para Glaser
[1981 *apud* @igliori_nocao_1999], essa lentidão ocorreu porque os
historiadores e educadores não deram importância para as dificuldades
presentes no ensino de números negativos.
Os PCN identificam como barreiras no ensino de números inteiros a
atribuição de significado às quantidades negativas. Dentre as
dificuldades, destaca-se o reconhecimento dos números em dois sentidos a
partir do zero, o reconhecimento e identificação do zero, origem e do
zero absoluto e a ideia intuitiva de que na operação de adição o
resultado é um número maior que o original e que na operação de
subtração o resultado é sempre menor [@pcn_1998].
## O uso de jogos no ensino
Portanto, considerando os obstáculos didáticos e epistemológicos
oriundos das operações com números inteiros e diante da limitação
apresentada pelo ábaco de números inteiros (material escolhido na
primeira proposta didática que elaboramos a respeito do tema), sugerimos
outra proposta de intervenção que tem como intenção proporcionar um
ensino significativo, em que o aluno tem papel ativo na sua
aprendizagem. Para isso, nos baseamos no uso de jogos, no qual buscamos
a compreensão para então formalizar o conteúdo, de modo a justificar a
utilização da regra de sinais.
> A introdução de situações contextualizadas, jogos e materiais
> manipuláveis, associadas ao uso da linguagem matemática, expressas em
> diversas possibilidades, viabilizam um trabalho didático que permite
> superar os obstáculos epistemológicos, ao esclarecer as escolhas
> realizadas ao longo do percurso de construção do conhecimento
> matemático envolvendo os Números Inteiros [@pommer_1998 p.4].
Corroborando com essa concepção, destacamos um trecho da Base Nacional
Comum Curricular (BNCC) que trata dos recursos didáticos e adverte que
estes devem servir para levar à reflexão e à sistematização:
> \[\...\] recursos didáticos como malhas quadriculadas, ábacos, jogos,
> livros, vídeos, calculadoras, planilhas eletrônicas e softwares de
> geometria dinâmica têm um papel essencial para a compreensão e
> utilização das noções matemáticas. Entretanto, esses materiais
> precisam estar integrados a situações que levam a reflexão e à
> sistematização, para que se inicie o processo de formalização [@bncc_2017, p. 276].
Vale destacar que o jogo não deve ser considerado apenas uma diversão ou
passatempo, ele deve ser planejado e executado com cuidado, como aponta
Fiorentini e Miorim [-@fiorentini_miorim_1996, p. 9]:
> O professor não pode subjugar sua metodologia de ensino a algum tipo
> de material porque ele é atraente ou lúdico. Nenhum material é válido
> por si só. Os materiais e seu emprego sempre devem estar em segundo
> plano. A simples introdução de jogos ou atividades no ensino da
> matemática não garante uma melhor aprendizagem desta disciplina.
Considerando o uso de jogos como estratégia de ensino, pela qual o aluno
desenvolve diversas habilidades, Smole, Diniz e Milani (2007, p. 9)
afirmam que isso ocorre porque "ao jogar, os alunos têm a oportunidade
de resolver problemas, investigar e descobrir a melhor jogada; refletir
e analisar as regras, estabelecendo relações entre os elementos do jogo
e os conceitos matemáticos".
Desta forma, o jogo, por ser um momento mais descontraído, pode
oportunizar um ensino sem pressão, o que facilita para os alunos
adquirirem os conhecimentos com mais significados e oferece um momento
de socialização da turma [@smole_diniz_milani_2007].
> Além disso, o trabalho com jogos é um dos recursos que favorece o
> desenvolvimento da linguagem, diferentes processos de raciocínio e de
> interação entre os alunos, uma vez que durante um jogo cada jogador
> tem a possibilidade de acompanhar o trabalho de todos os outros,
> defender pontos de vista e aprender a ser crítico e confiante em si
> mesmo [@smole_diniz_milani_2007, p. 9].
As atividades propostas nesta unidade didática têm como intuito
trabalhar as operações com números inteiros, como uma tentativa de
possibilitar aos alunos do 7° ano a compreensão das regras de sinais e,
assim, evitar que elas sejam apenas decoradas.
A primeira atividade consiste na manipulação de fichas, a fim de
familiarizar o aluno com as regras das operações de adição e subtração
de fichas. Já a segunda atividade trata-se de um jogo, que tem como
objetivo alcançar a transição da atividade concreta para a representação
na linguagem matemática na cartela que acompanha o jogo. Enquanto isso,
a terceira atividade, que também é um jogo, pretende possibilitar que os
alunos ultrapassem a ideia de que a operação de adição sempre aumenta e
que a operação de subtração sempre diminui. Por fim, ao desenvolver a
proposta didática, esperamos que os alunos compreendam as operações de
adição e subtração, assim como o motivo da regra dos sinais.
## Atividade 1:
[apresentação das operações por meio das fichas]{.small_h2}
Neste primeiro momento, apresentaremos as operações de adição e
subtração através de fichas coloridas. Essas fichas foram confeccionadas
levando em consideração as ideias do material manipulável conhecido como
Algeplan, principalmente na função que o sinal negativo realiza diante
das operações.
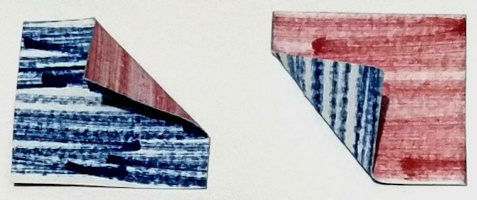
O professor disponibilizará aos alunos 20 quadrados com um dos lados do
quadrado de cor vermelha e outro azul^[5](#footnote-8){#footnote-ref-8}^
(@fig-frente_verso_fichas), de forma que, ao virar a ficha, troca-se de cor. Em seguida,
explicará como realizar as operações de adição e subtração utilizando as
fichas, assim como a regra de virar a ficha quando se está subtraindo.
{#fig-frente_verso_fichas fig-alt="Duas fichas: frente e verso, azul e
vermelho" loading="lazy"}
### Adição das fichas
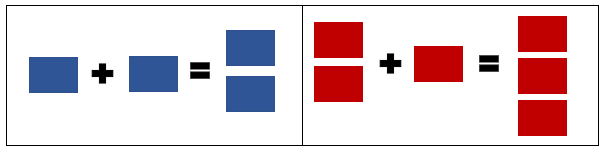
#### Adição de fichas de mesma cor:
Ao somar fichas de mesma cor, o valor final se dá pela quantidade de
fichas reunidas. A cor das fichas diz se esse valor é positivo ou
negativo. Veja o exemplo abaixo:
{#fig-adicao_fichas_mesma_cor fig-alt="Ilustração com fichas azuis sendo somadas e o mesmo com as
vermelhas" loading="lazy"}
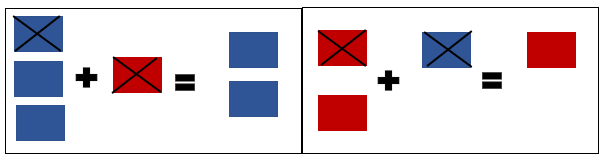
#### Adição de fichas de cores diferentes:
Vale ressaltar que fichas de cores diferentes se anulam, isto é, uma
azul se anula com uma vermelha. Após a anulação conta-se quantas fichas
sobraram e verifica-se a sua cor.
{#fig-adicao_fichas_cor_diferente fig-alt="Ilustração de fichas azuis e vermelhas sendo adicionadas. As fichas
que se anulam estão com um x" loading="lazy"}
### Subtração das fichas
Na subtração o sinal negativo tem a função de virar as fichas de lado e
trocar o sinal da operação. Observe que após a troca do sinal retorna-se
aos casos de adição. Veja os exemplos abaixo:
{#fig-subtracao_caso_1 fig-alt="Ilustração de fichas vermelhas e azuis invertendo o sinal - caso
1" loading="lazy"}
{#fig-subtracao_caso_2 fig-alt="Ilustração de fichas vermelhas e azuis invertendo o sinal - caso
2" loading="lazy"}
## Atividade 2:
jogo cartas das operações
O jogo *cartas das operações* levará os alunos a realizarem operações
com as fichas, seguindo as regras apresentadas anteriormente. A
atividade trabalha a visualização da operação com as fichas e, em
seguida, a passagem do material manipulável para a linguagem aritmética.
### Participantes:
2 jogadores.
### Objetivo da atividade:
Explorar e familiarizar o aluno com as regras das operações de adição e
subtração, utilizando as fichas, além de permitir a associação das
fichas com os números inteiros.
### Materiais
Para cada dupla de jogadores é entregue:
- 1 dado representando as operações de subtração e adição (@fig-dado);
- 42 cartas numeradas de 0 a 10 (20 positivas numeradas de 1 a 10, 20
negativas numeradas de 1 a 10 e 2 cartas com o número 0) com
representação visual colorida em cada carta, sendo
azul^[6](#footnote-9){#footnote-ref-9}^ a representação dos números
negativos e vermelho^[7](#footnote-10){#footnote-ref-10}^ dos
números positivos, como descrito nas fichas anteriores (@fig-cartas);
- Cartela 7x4 (@fig-cartela) para anotar resultados de cada rodada.
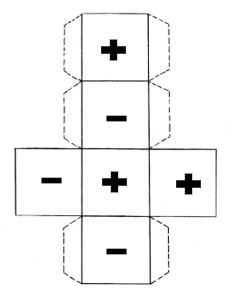{#fig-dado fig-alt="Dado para recortar e dobrar" loading="lazy"}
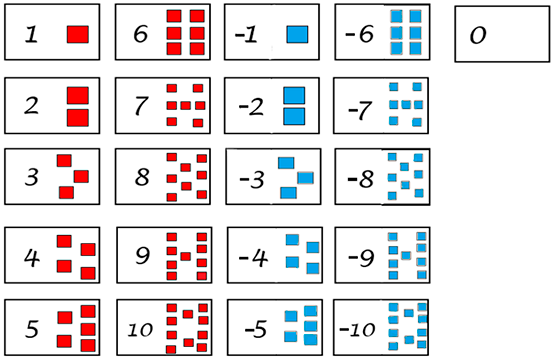{#fig-cartas fig-alt="Cartela com o número zero e mais vinte cartelas. Em cada uma das
cartelas aparecem retângulos e um número mostrando a quantidade de
retângulos. Nas que possuem retângulos azuis, o número fica negativo, já
nas que aparecem retângulo vermelhos,
não" loading="lazy"}
{#fig-cartela fig-alt="Tabela com 4 colunas: primeira carta, operação, segunda carta e
resposta. A tabela possui sete linhas a serem
preenchidas" loading="lazy"}
### Como jogar
1. A cada jogada, as 42 cartas numéricas são embaralhadas.
2. Cada jogador, na sua vez, deve retirar uma das 42 cartas do monte e
anotá-la na cartela entregue.
3. Em seguida, jogar o dado das operações e anotar a operação sorteada.
4. Novamente no montante de cartas embaralhadas, retirar outra carta e
anotar na cartela.
5. Com as informações anotadas na cartela, deve-se fazer o processo da
conta e anotar o resultado na coluna denominada de respostas.
6. Então o outro jogador realiza os mesmos passos, retirando a carta e
lançando o dado.
7. Repete-se o processo por 7 vezes (ou de acordo com o n° de linhas na
cartela).
8. Posteriormente o professor fará a correção para analisar os acertos
e erros, sendo atribuído um ponto a cada acerto. Para o resultado
errado da operação não será atribuído ponto algum.
9. O ganhador será o aluno que possuir o maior número de pontos.
10. Se houver empate, os alunos empatados jogam de novo, até surgir um
ganhador.
## Atividade 3:
jogo tabuleiro dos sinais
O jogo Tabuleiro dos sinais permite ao aluno perceber que a operação de
adição nem sempre aumenta, assim como a subtração nem sempre diminui,
uma das dificuldades de compreensão das operações com números inteiros.
Essa percepção será desenvolvida no decorrer do jogo, em que o aluno é
posto a competir e tentar criar estratégias para vencer.
### Participantes:
2 jogadores.
### Materiais
Cada dupla receberá:
- Peças do jogo: Dado das operações, as fichas coloridas e as cartas
utilizadas nas atividades 1 e 2;
- Tabuleiro da Fase 1 (@fig-tabuleiro_fase_1);
- Tabuleiro da Fase 2 (@fig-tabuleiro_fase_2).
- Um lápis.
O tabuleiro do jogo *Trilha dos Sinais* pode ser modificado de acordo
com as estratégias da aula elaborada pelo professor.
### Fase 1: tabuleiro 1
#### Objetivo do jogo
Explorar e investigar as diversas situações que possam surgir nas
operações de subtração e adição com números inteiros, por meio do jogo e
das fichas. O jogo permite que o aluno exercite o que aprendeu, até o
momento, sobre os números inteiros de forma lúdica.
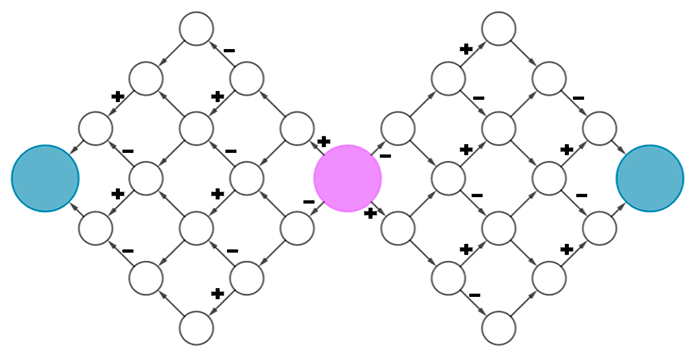{#fig-tabuleiro_fase_1 fig-alt="Tabuleiro com casa redondas (bolhas) com setas e indicação de operação
feita com os símbolos de positivo e
negativo" loading="lazy"}
#### Como jogar
1. Cada jogador recebe 21 cartas (@fig-cartas).
2. Cada jogador sorteia uma de suas 21 cartas. Na sequência, somam as
cartas sorteadas, para preencher o círculo central ou círculo de
origem, utilizando o lápis.
3. O jogador que tirou a maior carta inicia a partida e escolhe qual
lado do tabuleiro prefere jogar.
4. Para iniciar a partida o jogador irá escolher o caminho que seguirá.
5. O jogador 1, ao escolher um caminho em que a seta possui sinal
positivo ou negativo, deve sortear uma carta do monte e então
realizar a operação proposta pela seta. Por exemplo, se a seta tiver
sinal negativo, o jogador subtrairá o valor da carta sorteada com o
valor presente no círculo anterior à seta. Veja uma situação
representada abaixo:
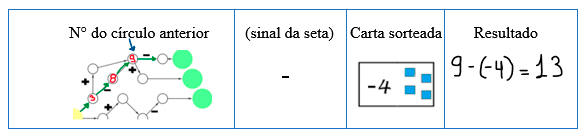{#fig-exemplo_1 fig-alt="Exemplo" loading="lazy"}
6. Se a seta escolhida não tiver sinal, o jogador deve jogar o dado de
operações para descobrir a operação a ser realizada e em seguida
tirar uma carta do monte. Então preencher o círculo indicado pela
seta com o resultado da operação realizada. Veja uma situação
representada abaixo:
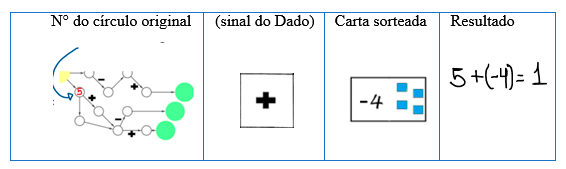{#fig-exemplo_2 fig-alt="Exemplo" loading="lazy"}
:::{.callout-note title="Observação" style="margin-left: 36px"}
O aluno pode utilizar as fichas coloridas para realizar essas operações, caso não se sinta confiante de realizar as contas sem utilizar o material.
:::
7. Agora é a vez do jogador 2. Ele realizará os mesmos passos descritos
para o jogador 1;
8. Na próxima operação, os jogadores devem realizar as contas levando
em consideração o resultado anterior. Por exemplo, se o resultado da
primeira operação foi 5 e a seta for de soma, terá que realizar a
seguinte conta: 5 + Carta sorteada e assim por diante.
9. Após seis jogadas, os jogadores completam o círculo final do
tabuleiro da Fase 1. Quem tiver um número maior no círculo final
será o vencedor. Se quiserem, os jogadores podem convencionar que o
vencedor será o que tiver o número menor.
### Fase 2: tabuleiro 2
#### Objetivo do jogo:
Mostrar para o aluno que trabalhar apenas com as fichas torna-se
insuficiente para o jogo, por exemplo, ao subtrair ou somar números
muito grandes, apontando a necessidade de trabalhar utilizando a regra
dos sinais.
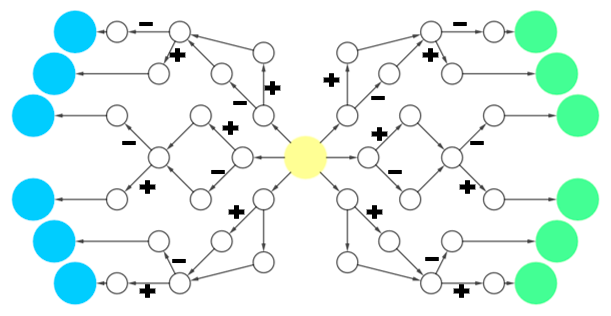{#fig-tabuleiro_fase_2 fig-alt="Tabuleiro com casa redondas (bolhas) com setas e indicação de operação
feita com os símbolos de positivo e
negativo" loading="lazy"}
#### Como jogar
1. O andamento do jogo ocorre da mesma maneira que a fase 1. Os
jogadores escolhem um caminho, se a seta tiver sinal, apenas retiram
uma carta do monte, e se a seta não tiver sinal os jogadores jogam o
dado de operações e retiram uma carta do monte.
2. Neste tabuleiro há seis círculos finais, logo realiza-se o jogo até
serem finalizados os seis caminhos.
3. Após completar os seis círculos finais, os jogadores devem somar os
valores presentes nestes círculos.
Caso os alunos estejam utilizando as fichas coloridas para auxiliar nas
operações, nesse momento a quantidade de fichas será insuficiente para
as operações com os números presentes nos círculos finais. Portanto, o
aluno precisa de um momento de análise das relações observadas, para que
após compreender o funcionamento do jogo dos sinais com as fichas, ele
possa reformular suas ideias e passar da representação com o material
para a representação com apenas números e símbolos. Pode ser também que
alguns alunos não utilizem as fichas em momento algum do jogo, fazendo
apenas a representação numérica.
Por meio do jogo, espera-se que os alunos possam compreender como os
valores das cartas, os seus sinais e a operação realizada interferem no
resultado da partida. Assim, por mais que em uma jogada o jogador tenha
dois números positivos grandes, dependendo da operação realizada, ele
pode obter um número menor que o esperado.
## Considerações finais
Com esta proposta consideramos que a compreensão do aluno sobre as
regras de sinais presentes nas operações de adição e subtração com
números inteiros será alcançada de maneira significativa, indo além da
simples memorização, pois os alunos terão a oportunidade de estabelecer
relações entre as fichas coloridas e a regra dos sinais. Espera-se
também que se desvinculem dos materiais manipuláveis e adotem uma
linguagem matemática ao expressar suas ideias. Essas ações favorecem que
os alunos exerçam um papel ativo no seu aprendizado.
Por conta da situação causada pela pandemia da COVID-19, não tivemos a
oportunidade de aplicar a proposta em sala de aula, mas propomos que os
professores utilizem as atividades com seus alunos, podendo alterá-las
conforme o contexto escolar.
## Notas
1. ::: {#footnote-4}
Acadêmica do curso de Matemática - Unioeste/Cascavel. Bolsista do
Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
E-mail: [↑](#footnote-ref-4)
:::
2. ::: {#footnote-5}
Acadêmico do curso de Matemática - Unioeste/Cascavel. Bolsista do
Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
E-mail: [↑](#footnote-ref-5)
:::
3. ::: {#footnote-6}
Acadêmica do curso de Matemática - Unioeste/Cascavel. Bolsista do
Programa Institucional de Bolsas de Iniciação à Docência (Pibid).
E-mail: [↑](#footnote-ref-6)
:::
4. ::: {#footnote-7}
Professora do curso de Matemática -- Unioeste/Cascavel. Coordenadora
de área do subprojeto Interdisciplinar Matemática/Química do
Programa Institucional de Bolsas de Iniciação à Docência da Unioeste
(Pibid). E-mail: [↑](#footnote-ref-7)
:::
5. ::: {#footnote-8}
Essas cores, nas tonalidades usadas, funcionam para daltônicos. Se o
leitor quiser alterá-las, lembre-se de usar *websites* ou *app* que
simulem os diferentes tipos de daltonismo de forma a não usar cores
que não são distinguidas por daltônicos. [↑](#footnote-ref-8)
:::
6. ::: {#footnote-9}
Veja a nota 5. [↑](#footnote-ref-9)
:::
7. ::: {#footnote-10}
Veja a nota 5. [↑](#footnote-ref-10)
:::
## Referências